The Dresden Codex Lunar Series and Sidereal Astronomy

Introduction

Herein, I assess Dresden Codex numbers and ancient Mesoamerican astronomy and calendar intervals generally in relation to sidereal astronomical cycles and intervals. Various entries appeared in series as ArchaeoBlog posts while I conducted the original research. This page permalinks those June 2009 posts and adds further reflections. Rather than deviate from that chronology, I continue posting the most recent research down page. The contents present the chronology as topics.

Contents

Dresden Codex Lunar Series
Long Count Intervals
819-Day Count
Dresden Codex Venus Table
Reflection
Related Readings

The Dresden Codex Lunar Series

2009.06.13 - The Dresden Codex Lunar Series presents a span of 11,457 days, equaling 11,292 degrees solar orbit. This amount has a sidereal correspondence with 857 days of lunar orbit motion (Table 1). Also, 11,457 lunar orbits equates to 857 solar orbits and 10,600 lunar synodic periods (moons). And, 857 full moon periods represents a precise integer number of earth rotations:

857.0 full moons
857.0 solar orbits

= 930.013 lunar nodal
= 11,457.016 lunar orbits

= 25,377.003 earth rotations
= 10,600.016 full moons

The "image series" of 11,457 days consists of the nine date intervals between ten images. The full ten intervals span 11,959 days, rather than the 11,960 days more accurately equaling 405 full moons. The 11,959 day interval also has a sidereal correspondence equating solar and lunar orbits. Angular lunar orbit motion during 897 earth rotations equals solar orbit motion during 11,959 days.

Table 1. Dresden Codex Lunar Series Astronomical Periods.
interval (TT)	degrees orbit		lunar periods
interval (TT)	solar	lunar	synodic	nodal	orbit
11,959 days	11,786.90		404.9700	439.4717
897 rotations		11,786.92
857 days		11,292.14
11,457 days	11,292.12		387.971	421.024
11,457 lunar orbits	308,519.6	4,124,520.0	10,600.001	11,503.08	11,457.000
857 solar orbits	308,520.0	4,124,525.3	10,600.015	11,503.09	11,457.015
857 moons		24,943.5	857.0	930.0128
25,377 rotations	24,943.512		856.9999	930.0129

Apparently, the focus of the lunar series is lunar nodal (the eclipses) and ratios far more accurate than either the Saros or Metonic eclipse periods represent or the eclipse intervals presented in the lunar series. Is sidereal astronomy the reason why the Maya astronomer utilized, instead of the Saros or Metonic eclipse cycles, a lunar series span of 11,457 days equaling 387.97 full moons? The accuracy of the sidereal ratios is very convincing:

The lunar series 11,457 and 11,959 day intervals are apparently based on sidereal astronomy. Is there any question that the Maya were doing sidereal astronomy? Hopefully, this new perspective presents a useful template, the stellar backdrop, upon which to now interpret the Dresden lunar series and other aspects of Native American astronomy.

2009.06.18 - The finding above prompted a closer look at some Long Count academic literature discussing both codices and stelae. To the best of my knowledge, Mesoamerican or any other prehistoric equation of lunar and solar orbit motions is a new consideration. I needed to amend my research applications for Long Count conversions and to do solar-lunar orbit conversions and comparisons.

In the Long Count glyphs at Uaxactun is a seven katun interval of 50,400 days, nearly equaling 138 years. A katun is a 7,200 day Mesoamerican calendar period consisting of 20 tuns of 360 days. A tun consists of 18 uinals of 20 days. The seven katun interval presents an equation of integer days of lunar and solar orbit motion (Table 2). Accuracy is within 20 minutes of lunar motion (1 : 1.000 003) when equating 50,400.0 days solar orbit (seven katuns) and 3,770.0 days lunar orbit. Seven katuns represents 138 tropical years less 3.4 days (1 : 1.000 068). By comparison, accuracy of the equation of 50,400 days solar orbit to 3,770 days lunar orbit is 1 : 1.000 003.

Seven katuns represents an integer equation of days and rotations; 50,538.0 rotations equals 50,400.0147 days. Accuracy of the 50,400 days to 50,538 rotations integer equation is 1.0 : 1.000 000 3, about 10 times more precise than the 50,400 days earth orbit to 3,770 days lunar orbit integer equation. Solar orbit for 3,770 days equates with 282 days of lunar orbit (1.0 : 1.000 004). An accurate sidereal commensuration exists between 138 solar orbits and 573 Mercury orbits (1.000 001). One-half of the seven katun period is well known in Maya astronomy:

An obvious question follows on these findings. Was the accuracy of the well-known seven katun interval improved upon over time, leading to observing solar and lunar eclipses in relation to the 11,457 and 11,959 day spans and their corresponding sidereal correlations?

2009.06.19 - A common Classic Maya cycle is the 819-day count, best known from Palenque, Quirigua, Copan, Tikal, and later from the Dresden Codex. Lunar orbit motion for 819 days equates to 10,949.0017 days of solar orbit (Table 3). Compared to integer days, accuracy is 1.0 : 1.000 000 4. Mean daily lunar motion is 13.17636 degrees, therefore the equation difference represents 25 seconds of lunar motion in comparision with 819 days. Draw a line from the center of the earth to the orbiting moon, and the difference, 0.0039 degrees, amounts to about 432m on the earth's surface in proportion to nearly 30 circumferences (29.976 lunar orbits = 819 days).

2009.06.24 - Another section of the Dresden manuscript has been termed the Venus Table. The 584-day intervals in the table closely correlate with the Venus synodic cycle. Subdivisions of the 584-day spans recongizably match the periodic appearances of the inner planet as Morning Star and Evening Star, albeit not precisely. Given 365 lunar orbits equals 10,000 rotations and 365 times eight-fifths equals 584, the 584-day period also correlates with lunar orbit; 584 days equals 21.3750 lunar orbits (Table 4) and just eight 584-day periods represents an integer number of lunar orbits. The 584-day increments express eights of lunar orbit.

The 365-day count is usually interpeted as the whole number approximation of the year. That is simply a coincidence. Only two fundamental sidereal motions can readily be counted, rotation and lunar orbit. Counting these two motions for just three decades reveals the ratios of 365 lunar orbits equaling 9999.71 rotations, 10,000 rotations equaling 365.01 lunar orbits, and 366 lunar orbits equaling 9999.73 days.

This sidereal equation, one of the most obvious and most neglected facts of ancient astronomy, is the foundation of accurate naked eye astronomy. It likely also is the sidereal foundation for the 584 day interval in the Venus Table and, combined with the regularity of earth rotations, a cosmic clockwork for observing the moon, Venus, and the other planets. Mean lunar orbit is a readily-visible, sidereal-referenced motion, especially compared to Venus observations.

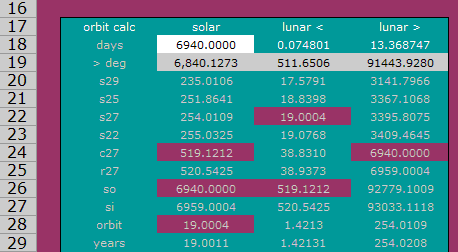
Given multiples of 365, integer lunar orbits do not equate until 855 lunar orbits with 23,360 days (64 times 365 = 40 times 584). Given 584 day modules (eight-fifths of 365), at one-fifth this interval 171 lunar orbits equate to 4,672 days (8 times 584).

The 584-day interval more accurately commensurates as a lunar number (Table 4). In 855 lunar orbits there are 23,360.022 days (1.0 : 1.000 001), compared to 40 Venus synodic periods with 23,357 days (40.0 : 40.00539 = 1.0 : 1.000 134). Even the Mars orbit cycle has a slightly more accurate commensuration (34.0 : 34.00391 = 1.0 : 1.000 115) than Venus synodic.

More will follow, no doubt, as I dig deeper. Meanwhile, I'm refining planetary orbital constants in my application. I do not want to assume the Maya were anything less than precise. I note modern astronomers were very recently formulating precise values of planetary orbit periods, and current references are not consistent. Too bad they burned all those Maya libraries!

2009.06.27 - The online version of archaeogeodesy.xls is updated. The new lunar-solar equation formulations and the planetary orbit conversions are in a worksheet. The AeGeo code is expanded with new terms. New Epoch v2009 versions will feature the same updates.

2009.06.30 - Epoch_Calc is online. The "calc" worksheet has an orbit calc table to equate lunar and solar orbit motion. You enter the number of days and read the calculations. Planetary orbits and their synodic cycles are now also converted. I've added new code terms for the planetary periods using the latest values available. Epoch Calc (250 KB), derived from archaeogeodesy.xls, is astronomy focused. The larger archaeogeodesy.xls application is focused on ancient monuments.

2010.01.03 - Addition to Table 3: the equation "819 solar orbits = 10,949 lunar orbits = 10,130 moons" represents an integer ratio of the orbits and moons. This accurate proportion likely determined use of 819 in astronomy counts, and infers a threshold date for knowledge of accurate orbital proportions. For integral solar orbits, 819 has a more integer-accurate ratio to both lunar orbits and moons than all smaller numbers except multiples of 160 orbits. I continue to discuss integer representation of astronomical ratios in Ancient Astronomy, Integers, Great Ratios, and Aristarchus.

2010.10.16 - Further consideration of the Maya "819-day" count revealed the integer equation of 819 years with 44 lunar standstill periods and 863 eclipse nodal intervals (1.0 : 1.000 001 65).

2012.02.01 - Bob Patten noticed a typo above, the lunar series span of 11,457 days now equals 387.97 full moons, a one-day correction matching the table value for same.

2012.08.08 - Portions of this page edited for clarity and precision using refined astronomy constants.