|
Eclipses in Archaeological and Early Historical Contexts
This section is intended to convey a general idea of the current history of eclipse knowledge. Astronomical data concerned with the cosmic objects which move along the ecliptic, the sun, moon, and the visible planets, is known from prehistoric cultures. The most remote eclipse record is likely a Rg-Veda description of a solar eclipse observed by Atri about 3,928 B.C. Before inventing paper, the Chinese kept records on bones and shells. Li Shu wrote about astronomy around 2,650 B.C. and observatory buildings are known by 2,300 B.C. Inscribed bones and tortoise shells from the Shang dynasty reference solar eclipses. From the Chou dynasty and the Warring States period, over 40 solar eclipse observations are recorded from 720 BC onward, the earliest recorded series.
"... the Spring and Autumn Annals records as many as 36 eclipses of the Sun. This series of observations, which commences with the event of Feb 22 in 720 BC, is the earliest from any part of the world ... prove to be in exact accord with those of eclipses listed in modern tables." Stephenson (1997:221-223) |
In Anyang, five recorded solar eclipses between 1,161 BCE and 1,226 BCE are known. Based on a Chinese inscription, astronomers from NASA's Jet Propulsion Laboratory (JPL) fixed the exact date and path of a solar eclipse in the year 1,302 B.C. to determine delta T, a measure of the slowing of the earth’s rotation. They concluded the length of each day was 0.0047 seconds shorter in 1,302 B.C.
An early Mesopotamian record of a total solar eclipse at Ugarit is from May 3, 1,375 B.C. Clay tablets with astronomical observations survive from Mesopotamian civilizations. Babylonian astronomical records on tablets dating from 1,700 B.C. report the motions of Mercury, Venus, and the Moon. Later records include a total solar eclipse on July 31, 1,063 B.C. and the well-documented Nineveh eclipse of June 15, 763 BC, recorded by the Assyrians. Diodorus of Sicily suggests ziggurats were the observation platforms. Continuous usage and layered rebuilding of ziggurats dates to the dawn of civilization.

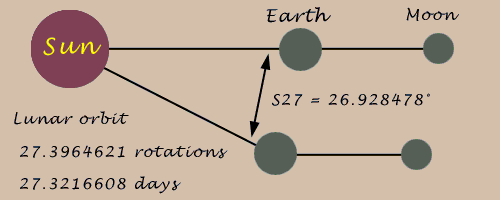
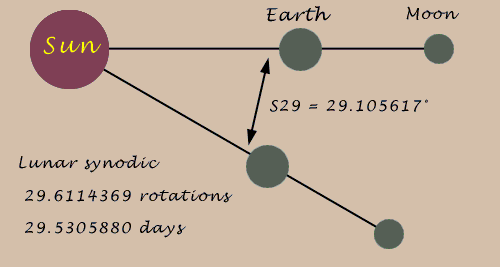
The Babylonian civil calendar was regulated by a Metonic cycle. The oldest record of the 223 moon Saros interval is Mesopotamian. The historical astronomy of Mesopotamia evidences, around 400 B.C., the celestial zodiac of 12 signs of 30 degrees each, a lunisolar calendar, a lunar synodic (full moon cycle) value of 29.530592644 days (as a fraction), knowledge of the Metonic and Saros eclipse cycles, eclipse record keeping, and use of arithmetical progressions for accurate eclipse prediction.
The Mesopotamian achievements evidence a long history of observations and the most advanced astronomy documented for the time. A great number of Mesopotamian astronomical texts from the last three centuries B.C. include evidence of sexagesimal place value notation, eclipse records, and the use of zero.
"... the eclipse observations made by medieval Arab astronomers are among the most accurate and reliable data from the whole of the pre-telescopic period." Stephenson (1997:456) |
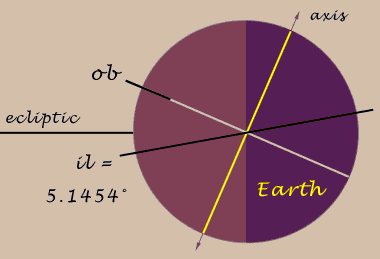
Astronomy also flourished in the Middle East and India during Europe's Dark Age. The 500 A.D. Indian book on astronomy, The Àryabhatiya of Àryabhata, evidences accurate astronomical knowledge in South Asia, in particular the precise sidereal ratio of the readily-observed earth rotations and lunar orbits. Àryabhata provided numerical and geometrical methods for calculating eclipses.
Eclipse calculations are evidenced by the Anikythera mechanism, a sophisticated mechanism dating from the 2nd century B.C and discovered near Crete in 1,900 by sponge divers. The mechanism's dials include a Metonic cycle calendar and a Saros eclipse-prediction dial with prediction glyphs. A Greek text by Archimedes on astronomical mechanisms has not survived. Homer's The Odyssey reports the 1,178 B.C. solar eclipse, "... the Sun has perished out of heaven, and an evil mist hovers over all."
The May 28, 585 B.C. total eclipse predicted by Thales in Asia Minor is the beginning of the Greek Classical Period. Greek historical documents evidence the role of Egyptian and Mesopotamian astronomy in Greek science. Ptolemy's Almagest included Babylonian observations of six solar eclipses, the earliest eclipse dating to 721 B.C. The Almagest also includes Egyptian sidereal observations of the moon and employs a Callippic calendar to date them.
Greek astronomer Meton and his associate Euctemon instituted a 19-year-eclipse calendar in Athens on the summer solstice of 432 B.C. Callippus' calendar cycle began astronomically in 330 B.C. on a start date when summer solstice and the lunar month beginning nearly coincided. In 330 B.C., new moon on June 28 was at 1:44 A.M. U.T. while solstice was close to midnight, less than two hours earlier. Geminus reports Callippus corrected the 19-year cycle, deducting one day every four Metonic periods. Apparently, Callippus knew of the one day difference between days per orbit and days per year every 4 Metonic cycles. This infers Callippus observed the Metonic cycle against sidereal reference. Aristarchus (Aristarchos) of Samos proposed a heliocentric solar system in 297 B.C. In the second century B.C. Hipparchos understood the elliptic orbit of the moon and precession of the equator.
"... the god visits the island every nineteen years, the period in which the return of the stars to the same place in the heavens is accomplished." Diodorus Siculus "the Greeks [who] use the nineteen-year cycle ...
are not cheated of the truth." Diodorus Siculus
76 * 365.25636 days per orbit = 27,759.48 days
76 * 365.24248 days per year = 27,758.43 days |
Greek records indicate an Egyptian practice of sidereal astronomy. Diodorus noted ancient Egyptian astronomers predicted solar eclipses. Thales, who brought Egyptian land surveying rules to the Greeks—the basis of Euclidian geometry, predicted the total solar eclipse on May 28, 585 B.C. According to historical documents, the Greeks had not predicted a solar eclipse prior to Thales predicting the eclipse near Miletus in Asia Minor. Thales studied mathematical and astronomical knowledge in Egypt before predicting the Miletus eclipse. Unfortunately, burning the Great Library in Alexandria destroyed untold Egyptian history.
|
"Timocharis, who observed at Alexandria, records that in year 36 of the first period according to Callippus, on Elaphebolion 15, which is Tybi 5, as the third hour was beginning, the moon overtook Spica with the middle of the part of its rim that points towards the equinoctial rising, and Spica traversed it, cutting off exactly one third of its diameter on the north side." |
The libraries in the Americas were also burned. Surviving Maya writing provides the best evidence of astronomy in pre-Hispanic America. Mayan symbols of the sun and the moon are unequivocally known. The 405 lunation eclipse cycle of 11,960 days is known from the Dresden Codex (810 nodal periods = 879 synodic periods or 1.0 : 1.000 010). From Copan Stelae 3 and A, the Metonic eclipse cycle is reported as 6,940 days, equaling 19 solar years and 235 moons. A sequence of bar and dot numerators in the Fejérváry Codex, pages 15 to 22, totaling 6,940 days, one Metonic cycle, was the first notice of this cycle in iconographic texts. The Metonic cycle also appears in the histories of Tilantongo and the Mixteca.
Knowledge of the eclipse cycle is evidenced in the House of the Sun at Palenque, dedicated in A.D. 692. The Palenque ratio is 81 moons to 2,392 days. Maya mathematics employed large integers instead of decimal notation. The 81 to 2392 ratio expresses a value of 29.530864 days per lunar cycle, 0.00028 days less than the present cosmic period. Longer Maya astronomical count intervals accurately equating solar and lunar orbits indicate early astronomical understandings. Evidence of lunar dates begin at A.D. 357 in an inscription from Uaxactun, bearing a Long Count date of 8.16.0.0.0. A vase from Uaxactun places the origin of a lunar calendar prior to A.D. 42.
In the Dresden Codex the Saros cycle was recognized. The most important codex is the Dresden with its eclipse series table. Eclipse prediction infers a certain level of knowledge, including the length of the lunar month, the interval between lunar nodes and the ecliptic limit for solar eclipses. Evidence of eclipse prediction infers this knowledge existed. About 200 lunar observations are known in Maya inscriptions.

|