Archaeogeodesy, a Key to Prehistory II, by James Q. Jacobs

Archaeogeodesy, a Key to Prehistory — Part Two

Ancient Earthworks of the
Eastern Woodlands Photo Galleries

The Popol Vuh, the ancient history of origins of the Quiche Maya, relates that the ancestors of the Quiche came to their side of the earth "on stones, as if there were no sea". When they arrived they "measured the earth and the sky" and they pointed to the heavens to indicate from whence they had come (as though to a certain position on a map?). Does this Quiche ethnohistorical document indicate a navigation ability enabling their migrations, or an ancient history of migration? We may never know what exactly the Popol Vuh account represents. Even though there is no remaining known written evidence of geodetic knowledge in the Americas during the prehistoric era, monuments, earthworks, and pyramids offer considerable evidence for study.

The Mound Builders of Eastern North America

Employing fundamental astronomy is how you survey, navigate or measure the earth. Astronomy is often evidenced in the most prominent archaeological features of the prehistoric American cultures—their thousands of earthworks, mounds and pyramids. In Eastern North America, the Adena, Hopewell and Mississippian cultures built earthen mounds, effigies, enclosures, truncated pyramids and diverse geometric forms. Due to their complexity, precision and magnitude, the largest of these earthworks rank among the most significant and enigmatic of ancient human monuments. During the past two centuries, most of these earthworks have been destroyed by the invasion of European culture groups who transformed the primordial landscape. Some of the sites have survived, particularly major monuments too immense to easily destroy. Some of these sites are similar to Neolithic mounds, henges and tumuli in the British Isles, but are not currently considered to be as ancient.

Grave Creek Mound, 80.744722W 39.916861N GPS

Fortunately E. G. Squier and E. H. Davis (1847), Cyrus Thomas (1894), and others undertook original surveys and explorations prior to the destruction of many sites. The Squier and Davis survey results, published by the Smithsonian Institution, include detailed illustrations of the sites. At present-day Newark, Ohio, two of the most impressive of all earthworks survive from a group that covered "an extent of about two square miles." Squier and Davis also stated, "These works are so complicated, that it is impossible to give anything like a comprehensive description of them." The Newark array of circles, a square, an octagon, parallel embankments and circular and elliptical mounds was the most diverse, extensive and complex of earthen monument sites. The background image of the previous page and the following graphic are based on Squier and Davis' Newark Works Map. (Thomas' 1894 map.)

The largest Newark feature, the Octagon State Memorial, or Newark Octagon, consists of a true circle 1,054 feet in diameter connected by 300 feet long parallel embankments to a large octagon enclosing 50 acres. The embankments are nearly six feet tall excepting the 14 feet tall by 170 feet long mound connected to the circle opposite its entrance from the Octagon. "Observatory Mound," so-called by Squier and Davis, overlooks the half-mile-plus long earthwork. At each of the angles of the Newark Octagon is a gateway and a truncated pyramid mound five feet high and measuring 80 by 100 feet at the base.

What I found to be the most impressive surviving feature at Newark was recently renamed the Great Circle Earthworks (Moundbuilders State Memorial), herein Newark Circle or Newark Great Circle, Squier and Davis described a 1,189 feet in diameter Newark Circle with walls nine feet high by 47 feet wide at the base surrounding an interior moat seven feet deep and 35 feet wide. Its grandeur is most impressive to the visitor at the entrance, where 100 feet long parallel entrance walls rise 16 feet above a 13 feet deep inner moat. At the center of the nearly 30 acre enclosure, Eagle Mound, four co-joined seven-feet-high mounds, arrow- or bird-shaped, about 150 feet long and 200 feet wide, aligns to the gateway. From this center perspective, the entrance azimuth frames the northerly lunar minor standstill. The entrance avenue of the 380-feet-wide earthen henge surrounding Stonehenge frames the Heel Stone and aligns near summer solstice sunrise.

At Newark the ratio of equal arc angles of latitude and longitude (1.301 to 1) forms a right triangle with a 52.452° obtuse angle. According to Thomas (1894), the Octagon's azimuth is 52.15° E. of N. The alignment of the Octagon earthwork also corresponds closely to the northerly lunar major extreme rise/set azimuth. Other possible, geometric rationales for the Octagon alignment are discussed in Temporal Epoch Calculations. The Newark and Marietta Earthworks site-to-site relationship, further discussed below, like the Octagon orientation, may infer Hopewell knowledge of the local latitude to longitude ratio.

I determined the coordinates of numerous Hopewell earthworks and Adena mounds by scanning 1:24,000 scale, 7.5-minute, USGS topographic maps at 600 dpi. This resolves to about 3.3 feet per pixel. Using Adobe Photoshop, I determined the coordinates of the centers of the site features to the nearest pixel. These were employed in a preliminary study. In 2005, I obtained GPS readings for many of the same features.

Marietta Conus Mound, 81.451556W 39.420333N GPS

Marietta Earthworks is located southeast of Newark near the Ohio River, at the mouth of the Muskingum River, the Newark area drainage. The Marietta and the Newark earthworks are the two largest Hopewell earthwork complexes. The largest earthwork at Marietta, the Marietta Square, measures about 1500 feet on a side. The largest Newark feature, the Octagon and connecting Circle, measures near 2900 foot in length.

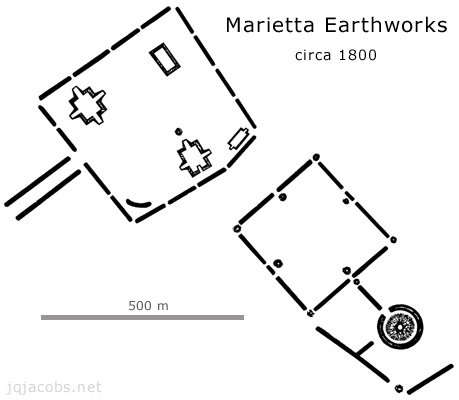I obtained the center point coordinate at Newark Octagon from the mean GPS readings at the eight vertices. At Marietta, I was able to determine the centerpoints of the three surviving major mounds. To plot relationships and determine approximte centerpoint coordinates for the Marietta squares, the GPS points and their coordinate grid were layered, using an Excel chart, on Squier and Davis' map as seen in the grahic below.

The distance from Marietta Square to Newark Octagon equals the circumference of the earth divided by days per year or orbit. Circumference divided by days per orbit (360°/365.25636) equals 0.98561° or earth's mean solar orbit per day (SO). The Marietta Square to Newark Octagon center-to-center arc distance is 0.98502° (0.9994 SO). This relationship infers possible precise knowledge of the size of the earth, the astronomic constants, and the distance between the sites, near 68 miles. The precise 1.0 SO arc length is marked in the graphic below, 65 m beyond the centerpoint. The long red line is the bearing from Marietta Conus and Capitolium Mounds to Newark Octagon. The vertical red line in the graphic presents a meridian precisely 0.98561° (1.0 SO) east of the Octagon centerpoint. The point where the exact arc length converges with this longitude lies between the two pyramid mounds (marked with the red asterisk) 76 m from the center of the square. From Newark Octagon to Marietta Capitolium, both the arc distance and the longitude difference equal precisely 1/365th of circumference (CIR/365). The arc distance from Newark Octagon to Quadranau Mound equals CIR/366.0.

The longitude difference aspect of the Marietta and Newark relationships suggests knowledge of the ratio of local latitude to longitude. Newark Octagon and the Marietta works are located at equal angular amounts of longitude difference and arc distance (the hypotenuse). The center-on-center arc distance from the Octagon to Marietta Capitolium (0.9863°) precisely equals their longitude difference (0.9864°). The ratios of degrees arc and longitude difference to the precise value CIR/365 are 1:1.000014 and 1:1.00010. The geodetic relationship of the two sites precisely expresses, on global scale, the local latitude to longitude proportion.

The features of the Newark Earthworks and the site-to-site relationships between Newark and Marietta offer more than sufficiently accurate evidence of possible knowledge of geodesy. Another aspect of the relationship is astronomical. The numbers 365 and 366 are associated with days and rotations as nearest integers to 365.25636, 366.25636, etc. They also present a fundamental astronomic ratio, as 365 and 366 lunar orbits per 10,000 days and rotations. The earthworks present modules of distances possibly based on astronomic constants and the size of the earth. The arc distance between these two large Hopewell earthworks, circumference divided by days per year/orbit, resembles the degree of measure based on days per year used by historical Chinese, CIR/365.25.

Newark Octagon, Observatory Mound, 82.450139W 40.051139N GPS

Monument Location as Evidence of Geodesy

This discussion has hinted at why sites might be located where they are, in discussing the geodetic properties of local latitudes, monument alignments and their spatial and distance relationships. Arc distance is constant except for the negligible influence of plate tectonics. Site-to-site arc distance remains fixed in landscape reference. In contrast, secular polar motion alters the actual latitude of almost all geodetic positions on the planet, very slowly changing latitude at a local rate. The change in latitude due to secular polar motion is very slow compared to the temporal change in latitude-determined solar and lunar illumination angles, a function of angle of inclination of the axis of rotation (obliquity). These temporal changes provide possible date-reaching mechanisms.

Cahokia, Monks Mound, Upper Terraces 90.062052W 38.6605208N GPS

Study of Monks Mound illustrates the methods and the possible utility of a site's latitude both as evidence of geodetic knowledge and as a date-reaching method. The geodetic latitude where the tangent of the angular relationship to the equator equals 0.80 is 38.65981 degrees. At Monk's Mound, the largest in volume prehistoric earthwork in the United States, the latitude today equals 38.6605208 degrees N. (center point, GPS mean of upper terraces). Given the formula for secular polar motion, I deduced the date the monument was positioned at exactly the 0.80 arc tangent latitude was around 1200 AD. This date is close to the radiocarbon date of the last constructs on the mound, the radiocarbon date and the polar motion dating agree. (At longitude 90.06184 degrees, local latitude shift per year equals 0.00000088 degrees given an annual polar shift of 0.00000097222 degrees along the meridian of 65.0 degrees west. Polar shift can be easily envisioned as the Andean landmass creeping northward about 10 cm per year. Recently, local plate motion modeling has refined and altered these findings slightly.)

Cahokia Woodhenge, Center, 90.075028W 38.659917N GPS

Monks Mound is an example of a monument situated in relation to a latitude's geometrical attribute, the latitude equals 0.80 arc tangent. Additionally, the latitude at which the solstice horizon rise and set angles equal 60 degrees (CIR/6) is near Monks Mound. Past writings by other authors have presented the possibility that the solar illumination geometry was the reason for Monks Mound's placement. However, the displaced position of the center post in Cahokia's Woodhenge indicates the builders understood that the local solstice swing was greater than 60 degrees. The latitude where the solstice angle equals 60 degrees is south of Cahokia, and was moreso earlier in time.

The latitude at which the solstice angle equals 60 degrees moves about 150 feet a year. Polar shift changes the position of the local latitude a few inches a year (the amount is different at different longitudes). In prehistoric time, without modern optics and theodolites, the task of determining latitude 'precisely' would have been both a challenge and an impressive accomplishment. The placement of Monks Mound, a millenia ago (or long before), with absolute precision at the 0.80 atan latitude, if purposeful, lucidly communicates the level of geodetic knowledge and the capabilities of the prehistoric Cahokians.

Newark Octagon 82.44426042W 40.05469621N GPS

Latitude versus Longitude

Latitude is far easier to determine than is longitude. Latitude is determinable using the angular relationship of geodetic position (local level/plumb) to the pole "star," a hypothetical, fixed, non-moving point in space. Geodetic latitude is determined by measuring the astronomic pole's position in angular relation to local level. From a fixed meridian of known latitude and scale, longitude determination by direct survey can be accomplished with geometry. Relationships of sites near each other, such as Newark and Marietta, can be directly surveyed. Two monuments located in such a survey system and evidencing knowlege of longitude do not necessarily infer astronomic determination of longitude.

Longitude can be solved astronomically by making a comparison of measurements of the position of a celestial object from two points on the earth using a temporal inter-reference of the measurements. Lunar eclipses provide a universal temporal reference. The longitude problem is easier on land (a fixed position) than at sea. On land observations can be averaged over long periods of measurement. Longitude could have been astronomically determined by prehistoric cultures on land.

In the modern era, the longitude problem was solved for the first time historically by development of accurate chronometers. Two clocks are set to the same time (i.e., noon at solar zenith) and one is transported to a second position. Comparison of the second clock with local solar time determines the longitude of the second position with reference to the first. The earliest longitude data derived by this method was only as accurate as the time the clocks kept. Due to their naval navigation needs, the British stimulated with monetary rewards the invention and development of accurate chronometers. This created a bias for a solution appropriate for a moving ship with an unknown position. On land, position is known and fixed, and therefore instantaneous determinations are not required.

The ocean navigation method for keeping accurate time that was in competition with chronometers was use of a lunar ephemeris. Mechanical chronometers won out because developments in metals technology surpassed astronomic understanding of the seemingly complex motions of the moon. Clocks are simply mechanical devices that serve as substitutes for the actual motions of the heavens. For navigation they are only as useful as they are accurate in their task of precisely paralleling the motions of the cosmos. With or without mechanical devices, determination of longitude ultimately depends on astronomy. Unlike the instantaneous determinations required from a moving ship on water, land determinations from fixed points can average measures over very extended periods of time, negating the complexities of lunar motion and constantly improving the accuracy of determinations.

Miamisburg Mound, 84.280886W 39.627597W

Part Three discusses fundamental astronomy and astronomically determined units of measure before returning to site relationships.